
W dzisiejszej odsłonie Szkoły Dziennikarstwa Danych przyglądamy się najczęstszym błędom popełnianym podczas pracy z danymi. Jak ich unikać? Odpowiadamy.
ROZDZIAŁ I: Podstawy dziennikarstwa danych
MODUŁ 1.7.: Uwaga! – częste błędy i sposoby ich unikania
O czym będzie mowa?
Mówi się, że istnieją trzy rodzaje kłamstw: kłamstwa zwykłe, duże kłamstwa i statystyka. To pokazuje, jakie mamy niekiedy podejście do danych liczbowych i sposobów ich prezentacji. I jest w tym trochę racji: dane w formie graficznej często były i wciąż są wykorzystywane do manipulacji faktami. Ale nie zawsze celowo. Każde dane istnieją w formie surowej, nieobrobionej. Mnogość informacji w nich zawartych powoduje, że trudno je zrozumieć. Dlatego wymagają obróbki. Ta z kolei wymaga selekcji danych. Te, które są odrzucane, są czasem najistotniejsze. Najczęściej pozostałe dane przedstawiają stan faktyczny, ale nie opisują całego kontekstu, nie opowiadają pełnej historii ukrytej w danych.
W tej odsłonie Szkoły Dziennikarstwa Danych porozmawiamy o pułapkach, które czyhają na wstępnych etapach obróbki danych. Jeśli je poznamy, łatwiej będzie ich unikać.
Pułapka średniej
Na pewno niejednokrotnie zetknęliście się ze zdaniem w stylu: “Statystyczny Europejczyk wypija litr piwa dziennie”. Czy kiedykolwiek zadaliście sobie pytanie, kim jest ten tajemniczy statystyczny Europejczyk i gdzie można go poznać? Zła wiadomość: nie można. Ona/on nie istnieje. W niektórych krajach spożywa się więcej wina niż piwa. Czy zatem w nich też wypija się litr piwa dziennie? A co z osobami, które w ogóle nie piją alkoholu? Albo z dziećmi? One również spożywają litr piwa każdego dnia? Oczywiście, że nie. Więc skąd biorą się takie stwierdzenia?
Ludzie je wypowiadający/piszący zwykle natrafiają na duże liczby, które chcą przybliżyć odbiorcom, np. każdego dnia w Europie spożywa się 109 mld litrów piwa. Ta dana wystarczy do stworzenia powyższego zdania (statystyczny Europejczyk wypija litr piwa dziennie). Liczbę dzieli się na liczbę dni w roku i na populację w Europie. Fascynujący nagłówek gotowy. My również korzystaliśmy z takich uproszczeń w poprzednich odsłonach Szkoły Dziennikarstwa Danych, ale należy pamiętać, że statystyczny nie znaczy każdy. Oznacza to tylko tyle, że niektórzy piją więcej, a niektórzy mniej. Średnia ma sens, ale pod warunkiem, że dane są rozłożone normalnie. Co to znaczy? Poniższy wykres przedstawia trzy rożne rozkłady normalne. Wszystkie mają taką samą średnią, a jednak są wyraźnie odmienne. To, czego nie pokaże nam średnia, to zakres danych.
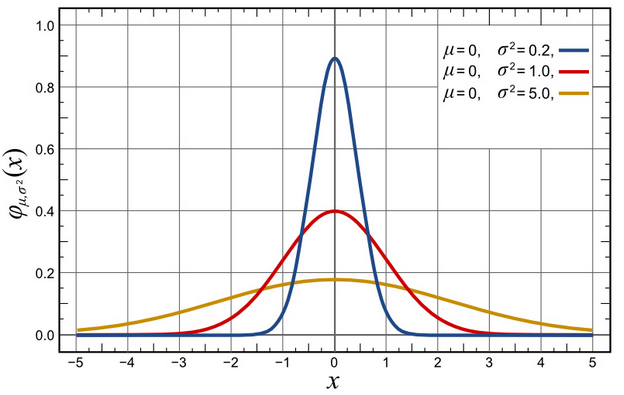
W większości przypadków nie mamy do czynienia z normalnym rozkładem. Dobrym przykładem są wynagrodzenia. Średnie wynagrodzenie może sugerować, że połowa osób zarabia więcej, a druga połowa – mniej, niż wynosi średnia. A to nieprawda. Znaczna część ludzi zarabia poniżej średniej. Dane dotyczące wynagrodzeń nie mają normalnego rozkładu. Zwykle wygląda on tak jak na poniższym wykresie.
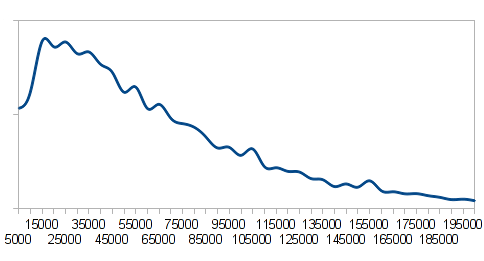
Wzrost średniej zarobków nie oznacza wcale, że wszyscy zarabiają coraz więcej. Najczęściej średnią zawyża wąskie grono najbogatszych, pomnażających swoje majątki.
Ekonomiści, zdając sobie sprawę z tego problemu, wymyślili wskaźnik, który ma reprezentować dystrybucję dochodów. Mowa o współczynniku Giniego. Sposób jego obliczania jest dość skomplikowany, ale warto się z nim zapoznać. Piszemy o nim, byście pamiętali, że wiele informacji umyka naszej uwadze, jeśli posługujemy się wyłącznie średnią. Bądźcie czujni, czytając nagłówki w stylu “Statystyczny Europejczyk wypija litr piwa dziennie”.
Więcej niż średnia
Skoro czasem średnia zniekształca odbiór danych, to z czego należy korzystać?
– Zestawcie średnią z konkretnym przedziałem. Lepiej powiedzieć np., że konkretna część Europejczyków pije pół litra piwa dziennie niż twierdzić, że statystyczny Europejczyk spożywa litr tego trunku każdego dnia.
– Użyjcie mediany. Czym ona jest? Pisaliśmy o tym w części pt. Matematyka dla opornych.
– Użyjcie kwartyli lub percentyli.
Rozmiar ma znaczenie
W świecie wizualizacji danych rozmiar ma znaczenie. Spójrzcie na dwa poniższe wykresy, obrazujące wydatki na opiekę zdrowotną w Finlandii.
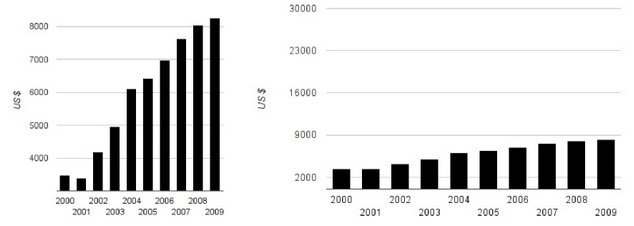
Wyobraźcie sobie nagłówki prasowe oparte o oba wykresy. W przypadku tego z lewej strony, mogłyby brzmieć tak: “Wydatki na opiekę zdrowotną w Finlandii drastycznie rosną”. W przypadku wykresu z prawej: “Wydatki na opiekę zdrowotną w Finlandii od lat na stałym poziomie”. A teraz przyjrzyjcie się wykresom raz jeszcze. Oba (w zły sposób) przedstawiają ten sam zestaw danych.
W pierwszym wykresie zakres osi pionowej nie zaczyna się od zera. Właśnie ta manipulacja sprawia, że różnica pomiędzy poszczególnymi latami wydaje się tak znacząca (wydatki w 2002 r. “wzrosły trzykrotnie” w porównaniu z poprzednim rokiem). Problemem drugiego wykresu jest również nieodpowiedni dobór zakresu. Bo choć oś y rozpoczyna się od zera, to kończy na 30 tys. Przy największych wartościach oscylujących w granicach 8 tys. to zdecydowanie zbyt duża wartość.
Oba te przykłady pokazują, jak ważny jest sposób wizualizacji danych. Oto trzy podstawowe reguły, których należy się trzymać:
– Korzystaj z odpowiedniego zakresu. W bardzo niewielu przypadkach oś y powinna zaczynać się od wartości innych niż zero.
– Zawsze podpisuj osie, by odbiorcy wiedzieli, co i w jakim zakresie reprezentują.
– Zmiany w wielkościach poszczególnych elementów wykresu muszą odpowiadać zmianom wartości z naszej bazy danych. Jeśli zatem wartość A wynosi 1, a wartość B – 2, to reprezentujące je fragmenty wizualizacji muszą spełniać ten sam warunek – B musi być dwukrotnie większe od A.
Czas pokaże
Podczas prezentacji danych osadzonych w czasie, kluczowa jest nie tylko oś y, ale również x. Spójrzcie na poniższy wykres reprezentujący wydatki na opiekę zdrowotną w Finlandii.
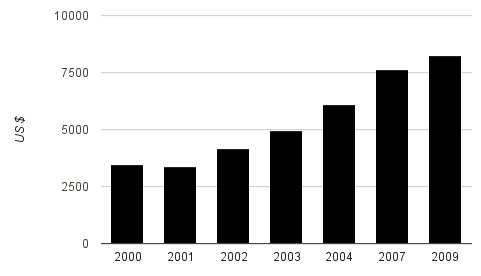
Czyżby wynikało z niego, że od 2002 r. mamy do czynienia ze stałym, corocznym wzrostem wydatków na opiekę zdrowotną? Nie, choć wizualizacja to sugeruje. Zerknijcie na podpisy osi poziomej. Zwróciliście uwagę, że do 2004 r. wartości podawane są w rocznych odstępach, a później się to zmienia? Jeśli zatem chcecie zbadać jakieś trendy, upewnijcie się, że odstępy pomiędzy poszczególnymi wartościami (osi x) są takie same.
Korelacja to nie związek przyczynowo skutkowy
To zdanie mówi samo za siebie i nie wymaga komentarza. Pamiętajcie, że korelacja pomiędzy jakimiś wartościami nie oznacza, że jedna wartość wpływa na drugą. Bo czy np. fakt, że w grudniu rośnie sprzedaż butów i samochodów oznacza, że powodem rosnącego popytu na auta jest rosnący popyt na obuwie?
Kontekst, kontekst i jeszcze raz kontekst
Jedną z bardzo ważnych rzeczy podczas pracy z danymi jest nadanie im kontekstu. Bez niego liczby nic nie znaczą. Wyjaśnijcie, co chcecie pokazać, jak czytać dane/wizualizacje, skąd dane pochodzą i co z nimi zrobiliście. Jeśli nadacie danym właściwego kontekstu, wnioski przyjdą same.
Procent kontra punkt procentowy
W tę pułapkę wpadamy dość często. Jeśli wartość dawniej wynosiła 5 proc., a obecnie wynosi 10 proc., to o ile się zmieniła? Jeśli Wasza odpowiedź brzmi: o 5 proc., to jesteście w błędzie. Odpowiedź brzmi: o 100 proc. (10 proc. to 200 proc. 5 proc.). Na to samo pytanie można odpowiedzieć: o 5 punktów procentowych. Zwracajcie na to uwagę, czytając nagłówki prasowe lub sami je tworząc.
Wszystkie kursy z cyklu Szkoła Dziennikarstwa Danych znajdziecie tutaj: Darmowe kursy dziennikarstwa danych.
Tłumaczenie: Piotr Kozłowski – Datablog.pl
Tekst został opublikowany na licencji CC BY-SA 3.0.
Źródło: School of Data








